|
Há
muito tempo se observou que certos corpos tem a
propriedade de atrair o ferro. Esses corpos foram
chamados ímãs. Essa propriedade dos ímãs foi observada
pela primeira vez com o tetróxido de triferro (  ), numa região da Ásia, chamada Magnésia. Por causa
desse fato esse minério de ferro é chamado magnetita, e os
ímãs também são chamados magnetos.
), numa região da Ásia, chamada Magnésia. Por causa
desse fato esse minério de ferro é chamado magnetita, e os
ímãs também são chamados magnetos.
Ímãs naturais e artificiais
|
A
magnetita é o ímã que se encontra na natureza: é o ímã
natural. Mas, podemos fazer com que os corpos que
normalmente não são ímãs se tornem ímãs. Os ímãs obtidos
desse modo são chamados ímãs artificiais. Chamamos corpo
neutro àquele que não tem propriedade magnética: corpo
imantado àquele que se tornou ímã. Chamamos imantação ao
processo pelo qual um corpo neutro se torna
imantado. Teoricamente, qualquer corpo pode se tornar um
ímã. Mas a maioria dos corpos oferece uma resistência
muito grande à imantação. Os corpos que se imantam com
grande facilidade são o ferro e certas ligas de ferro
usadas na fabricação de ímãs permanentes. Uma dessa ligas
é o ALNICO, composta de ferro, alumínio, níquel, cobre e
cobalto.
Os principais processos de imantação são:
a. Por indução magnética
É o fenômeno pelo qual uma barra de ferro se imanta quando fica próxima de um ímã.
b. Por atrito
Quando uma barra de
ferro neutra é atritada com um ímã, ela se
imanta. É necessário que sejam atritados sempre no mesmo
sentido, porque o atrito num sentido desfaz a ímantação
obtida no outro.
c. Por corrente elétrica
Suponhamos que um
condutor seja enrolado em uma barra de ferro e
percorrido por uma corrente elétrica; a barra de ferro se
torna um ímã. Como a imantação foi obtida por meio de uma
corrente elétrica, esse ímã é chamado eletroímã. Os eletroímãs são bastante comodos por dois
motivos: 1o) conseguimos obter eletroímãs muito mais possantes do que os ímãs naturais; 2o)
podemos fazer um verdadeiro controle do eletroímã,
controlando a corrente que passa por ele; assim,
aumentando a intensidade da corrente, o eletroímã se torna
mais possante; suprimindo-se a corrente, ele deixa de
funcionar, etc..
Ímãs permanentes e temporais
|
De
acordo com a constituição química do ímã artificial,
ele pode manter a propriedade magnética por muito
tempo, até por muitos anos, ou perdê-la logo depois que
cesse a causa da imantação. No primeiro caso o ímã é
chamado permanente; no segundo, ímã temporal, ou
transitório. Os eletroímãs são sempre ímãs temporais. Os
ímãs naturais são permanentes.
|
Regiões polares
|
Um ímã não
apresenta propriedades magnéticas em toda a
sua extensão, mas só em certas regiões,
chamadas regiões polares. Quando o ímã tem forma
de barra as regiões polares são as extremidades da
barra. Entre as regiões polares há uma região
que não possui propriedades magnéticas: é chamada
região neutra.
Quando um ímã
é suspenso pelo seu centro de gravidade,
entra em oscilação e depois fica em
equilíbrio numa posição tal que suas regiões
polares ficam voltadas para os polos geográficos
da Terra. Chamamos região polar norte do ímã
àquela que é voltada para o polo norte geográfico,
quando o ímã é suspenso pelo centro de gravidade;
região polar sul àquela que é voltada para o polo
sul geográfico, quando o ímã é suspenso pelo
centro de gravidade.
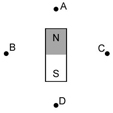
Atração e repulsão
|
Consideremos dois
ímãs suspensos pelos centros de gravidade.
Aproximando as suas regiões polares de todas as maneiras
possíveis, concluímos o seguinte princípio, demonstrado
exclusivamente pela experiência: “duas regiões polares de
mesmo nome se repelem, e de nomes contrários se atraem”
|
De
acordo com o critério adotado para dar os nomes às regiões
polares, concluímos que o polo norte geográfico da Terra é
uma região polar sul magnética; e que o polo sul
geográfico é uma região polar norte magnética.
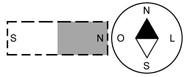
Essa propriedade dos
ímãs de se orientarem sempre para os polos terrestres
é que permite que os ímãs sejam usados como
bússolas. A lâmina magnética é um ímã artificial obtido
com uma lâmina de aço de forma de losângulo. A
bússola já era conhecida pelos chineses, parece que pelo
ano 120 D.C.. No século XI começou a ser
usada em navegação. A bússola é uma lâmina magnética
adaptada a uma “rosa dos ventos”.
Curiosidades
~Tipos de ímãs:
Com o desenvolvimento industrial, no século passado, tornou-se necessário obter ímãs mais potentes para diversos usos. O primeiro deles criado na década de 1930, recebeu o nome de alnico, que são as iniciais dos elementos acrescidos ao ferro: alumínio, níquel e cobalto. As principais características desse tipo de ímã são sua funcionalidade a altas temperaturas ( de 500ºC a 550ºC) e a grande res istência a corrosão. Veja esse tipo de ímã abaixo:
Nos anos de 1950, foi criado o ímã cerâmico (ferrite), que é resistente a corrosão, sais lubrificantes e gases. Sua temperatura de trabalho está em torno de 250ºC e é utilizado, por exemplo, em alto-falantes. Observe esse tipo de ímã:
Nos anos 1960, trabalhando com elementos das terras-raras criou-se o ímã samário-cobalto. Ele possui
excelentes propriedades magnéticas, é funcional a temperaturas de até 250ºC, mas é oneroso e frágil. É utilizado, por exemplo, em micro motores. Esse tipo de ímã está representado da foto abaixo:
Os ímas de neodímio-ferro-boro foram criados a partir da década de 1980, e são os mais modernos em uso, pois possuem as melhores qualidades magnéticas. Porém são suscetíveis à corrosão e sua temperatura funcional, é normalmente abaixo de 200ºC. São utilizados em alto-falantes, equipamentos elétricos e brindes. Veja abaixo esse tipo de ímã:
~A história da bússola
Há mais de mil anos os chineses criaram um dispositivo que lhes permita orientação geográfica em suas viagens , tanto em terra quanto no mar. Esse dispositivo atualmente é denominado bússola magnética ou simplesmente bússola (os marinheiros chamam também de agulha).
A bússola chinesa ( considerada "sagrada" ou "mágica") era composta de uma mesa quadrada e uma colher de magnetita, apoiada sobre um pino que apontava na direção sul, como o imperador, que, sentadono norte do palácio, olhava para o Sul ( na cultura chinesa , o norte tem um significado muito importante). Então, por meio da orientação da colher, conhecia-sed aproximadamentea direção norte-sul.
O desvio que existe ent re o norte magnético e o sul geográfico (ou entre o sul magnético e o norte geográfico) é denominado declinação magnética. Existem relatos a respeito do conhecimento desse desvio desde o século XV. O processo para determinar a declinação, naquela época, baseava-se na observação da estrela Polar no hemiférico norte ou da estrela do Pé do Cruzeiro no hemisférico sul, que deu origem à expressão "bornear" a bússola.
No século XVI, quando se descobriu que os metais nas proximidades da bússola poderiam interferir na orientação da agulha, começou-se a produzir-las envoltas em caixas de madeira.
hoje em dia, as bússolas continuam sendo largamente utilizadas em navios, aviões e por aventureiros para servir de orientação durante as viagens, complementando o GPS.
Magnetismo - O Campo magnético
O campo magnético
|
Chama-se
campo magnético de uma massa magnética à região que
envolve essa massa, e, dentro da qual ela consegue exercer
ações magnéticas. Já vimos que não existe na natureza
uma massa magnética isolada, porque um polo norte
sempre aparece associado a um polo sul. Desse modo, o
campo magnético do polo norte de um ímã está sempre
influenciado pelo polo sul do mesmo ímã. Mas, para
facilidade de estudo, consideraremos em primeiro lugar o
campo magnético de um polo único. Para isso temos de
considerar ímãs suficientemente alongados para que
possamos desprezar a influência de um polo sobre o outro.
|
Propriedade fundamental do campo magnético
|
Seja o campo
produzido pela massa magnética M.
Suponhamos que num ponto A desse campo seja colocada
a massa magnética puntiforme m, suficientemente
pequena para não alterar o campo magnético de M
(fig. 235). Em m atuará uma força  , que pode ser de atração ou repulsão, de acordo
com os sinais de M e m. Suponhamos que retiremos do
ponto A a massa magnética m e coloquemos nesse
mesmo ponto, sucessivamente, as massas
magnéticas
, que pode ser de atração ou repulsão, de acordo
com os sinais de M e m. Suponhamos que retiremos do
ponto A a massa magnética m e coloquemos nesse
mesmo ponto, sucessivamente, as massas
magnéticas  , todas elas satisfazendo as duas condições:
puntiformes, e suficientemente pequenas para não
alterarem o campo de M. Nessas massas atuarão,
respectivamente, as forças
, todas elas satisfazendo as duas condições:
puntiformes, e suficientemente pequenas para não
alterarem o campo de M. Nessas massas atuarão,
respectivamente, as forças  . A propriedade fundamental do campo magnético é a
seguinte: o quociente dessas forças pelas
massas magnéticas correspondentes colocadas em
A é uma grandeza vetorial constante em módulo,
direção e sentido, para o mesmo ponto A
. A propriedade fundamental do campo magnético é a
seguinte: o quociente dessas forças pelas
massas magnéticas correspondentes colocadas em
A é uma grandeza vetorial constante em módulo,
direção e sentido, para o mesmo ponto A
|
|
 (constante) (constante)
Essa grandeza vetorial  é chamada vetor campo magnético, ou simplesmente, o
campo magnético no ponto A. Considerando só uma
igualdade, temos:
é chamada vetor campo magnético, ou simplesmente, o
campo magnético no ponto A. Considerando só uma
igualdade, temos:
 ou ou 
A equação  do campo magnético é a que corresponde à equação do campo magnético é a que corresponde à equação  do campo elétrico, e do campo elétrico, e  do campo gravitacional (veja o tópico "Propriedade Fundamental do Campo Elétrico" ).
Considerando os módulos de do campo gravitacional (veja o tópico "Propriedade Fundamental do Campo Elétrico" ).
Considerando os módulos de  e m, temos:
Quando e m, temos:
Quando
 , resulta , resulta 
Significa que o
módulo do campo magnético em um ponto é igual à
intensidade da força que atua sobre a unidade de massa
magnética colocada nesse ponto.
A equação  mostra que a força que atua na massa magnética m
colocada em um campo magnético depende de dois fatores:
mostra que a força que atua na massa magnética m
colocada em um campo magnético depende de dois fatores:
1o) da própria massa m;
2o) do fator vetorial  , que não depende de m, mas sim do ponto em que ela é colocada.
Recorde o tópico "Propriedade Fundamental do Campo Elétrico" . , que não depende de m, mas sim do ponto em que ela é colocada.
Recorde o tópico "Propriedade Fundamental do Campo Elétrico" .
Características do vetor campo H
| Η |
Características do vetor campo H
1. Significado físico
 é o quociente de uma força por uma massa magnética. é o quociente de uma força por uma massa magnética.
2. Módulo
No
cálculo do módulo suporemos que a massa magnética M que
produz o campo seja puntiforme. Repetindo o raciocínio
desenvolvido no tópico "Características do Vetor Campo"
para o caso do campo elétrico podemos provar que, sendo d
a distância da massa magnética M ao ponto A, o módulo
do campo magnético em A é
onde  é a permeabilidade magnética do meio em que se produz o campo. é a permeabilidade magnética do meio em que se produz o campo.
3. Direção
O campo magnético é também um campo newtoniano. O vetor  tem a direçao da reta MA. tem a direçao da reta MA.
4. Sentido
Analogamente ao caso
de campo elétrico, podemos provar que: quando M é
positiva, isto é, é massa magnética de um polo norte,
o sentido de  é o sentido MA; quando M é negativa, isto é, é massa magnética de um polo sul, o sentido de é o sentido MA; quando M é negativa, isto é, é massa magnética de um polo sul, o sentido de  é o sentido AM é o sentido AM
|
Observações
Pelas características de  vemos que essa grandeza vetorial depende
exclusivamente da massa magnética M, da
permeabilidade
vemos que essa grandeza vetorial depende
exclusivamente da massa magnética M, da
permeabilidade  e da distância d. E não depende da massa
magnética m, que tínhamos suposto colocada em A
para definirmos
e da distância d. E não depende da massa
magnética m, que tínhamos suposto colocada em A
para definirmos  . Esse fato já está contido na definição de . Esse fato já está contido na definição de  , porque quando dizemos que o quociente , porque quando dizemos que o quociente  é constante, queremos dizer que ele não depende de é constante, queremos dizer que ele não depende de  nem de m. nem de m.
Unidades de intensidade de campo
|
a. Sistema CGSES
É obtida da equação  considerando-se considerando-se  e e  .
Resulta:
Um
oersted é a intensidade do campo magnético em um
ponto tal que, a massa magnética de uma .
Resulta:
Um
oersted é a intensidade do campo magnético em um
ponto tal que, a massa magnética de uma  , colocada nesse ponto fica sujeita à força de um dine. , colocada nesse ponto fica sujeita à força de um dine.
b. Sistema MKS
Considerando:
 resulta:
Recordemos que a unidade de massa magnética do sistema MKS também pode ser expressa por
resulta:
Recordemos que a unidade de massa magnética do sistema MKS também pode ser expressa por  . Como consequência, a unidade de intensidade de campo também pode ser expressa assim:
Um . Como consequência, a unidade de intensidade de campo também pode ser expressa assim:
Um  é a intensidade do campo magnético num ponto tal que a
massa magnética puntiforme de um weber colocada nesse
ponto fica sujeita à força de um newton.
é a intensidade do campo magnético num ponto tal que a
massa magnética puntiforme de um weber colocada nesse
ponto fica sujeita à força de um newton.
|
Campo de mais que uma massa magnética pontual
|
Quando
o campo magnético é produzido por mais que uma massa
magnética puntiforme, calculamos o vetor campo
produzido por cada massa magnética e depois efetuamos a
soma vetorial de todos esses campos. Considerando o campo
de duas massas magnéticas  e e  , em um ponto A teremos: o campo , em um ponto A teremos: o campo  , devido a , devido a  , valendo:
O campo , valendo:
O campo  , devido a , devido a  , valendo:
O campo resultante será , valendo:
O campo resultante será  tal que: tal que:
|

É este o
caso de um ímã não muito comprido, tal que não podemos
desprezar a influência de nenhum dos polos. Em um ponto A
o polo norte produz um campo  . No mesmo ponto o polo sul produz um campo . No mesmo ponto o polo sul produz um campo  . Então, o campo resultante . Então, o campo resultante  é a soma vetorial de é a soma vetorial de  com com  : :

Linha de força
|
Chama-se
linha de força de um campo magnético a uma
linha que em cada ponto é tangente ao campo
 desse ponto (fig. 239).
Vemos que
essa definição é idêntica à definição de
linha de força do campo eletrostático. As
características das linhas de força do campo
magnético são as mesmas das linhas de força do
campo elestrostático, a saber (veja o tópico
"Linha de Força" ): desse ponto (fig. 239).
Vemos que
essa definição é idêntica à definição de
linha de força do campo eletrostático. As
características das linhas de força do campo
magnético são as mesmas das linhas de força do
campo elestrostático, a saber (veja o tópico
"Linha de Força" ):
|
|
|
1a) Duas linhas de força de um campo magnético nunca se cruzam.
2a) As
linhas de força do campo magnético produzido por
uma única massa magnética seriam retilíneas. E as
do campo produzido por mais que uma massa magnética são
curvas. Como na natureza não existe uma massa
magnética isolada, mas elas existem aos pares, formando
os ímãs, concluímos que as linhas de força dos campos
magnéticos dos ímãs são curvas. A figura 239 mostra a
forma das linhas de força do campo de ímã em forma de
barra.
3a)
Convencionamos que o sentido da linha de força seja o
sentido de deslocamento de uma massa magnética
puntiforme norte colocada sobre a linha. Com essa
convenção concluímos que as linhas de força “saem”
do polo norte e “entram” no polo sul.

a. Tubo de força
Chama-se tubo de
força ao conjunto das linhas de força que passam
pelos pontos de uma linha fechada não plana
considerada no campo. É conceito análogo ao do campo
eletrostático (veja o tópico "Tubo de Força" ).
b. Campo magnético uniforme
É aquele em que o campo  tem mesmo módulo, mesma direção e mesmo sentido em todos os pontos.
As linhas de força desse campo são retas e paralelas (compare com o tópico "Campo Elétrico Uniforme").
Na prática se obtém um campo magnético
uniforme com um ímã que tenha os polos
planos e paralelos. O leitor deve estar lembrado de que, para
se produzir um campo elétrico uniforme se usam
dois planos uniformemente eletrizados, paralelos
e próximos, um com carga tem mesmo módulo, mesma direção e mesmo sentido em todos os pontos.
As linhas de força desse campo são retas e paralelas (compare com o tópico "Campo Elétrico Uniforme").
Na prática se obtém um campo magnético
uniforme com um ímã que tenha os polos
planos e paralelos. O leitor deve estar lembrado de que, para
se produzir um campo elétrico uniforme se usam
dois planos uniformemente eletrizados, paralelos
e próximos, um com carga  , outro com , outro com  : veja : : veja :
Espectros magnéticos
|
Podemos conhecer
praticamente o aspecto das linhas de força do campo
magnético de um ímã. Basta colocar sobre o ímã uma
folha de cartão; depois espalhar sobre o cartão um pouco
de limalha de ferro. Os pequenos pedacinhos de ferro se
imantam: cada um deles se torna um ímã. O polo norte de
cada um desses pequenos ímãs é atraído pelo polo sul do
vizinho, de maneira que se formam verdadeiras cadeias de
ímãs. Essas cadeias se dispõem sobre o cartão
exatamente ao longo das linhas de força. Chama-se
espectro magnético à figura obtida com a limalha de ferro
assim disposta ao longo das linhas de força. A primeira figura
mostra o espectro magnético de um ímã em forma de barra; a
segunda figura 242 é a fotografia do espectro de um ímã em forma
de ferradura.
|
Ímã colocado em um campo magnético uniforme
|
Suponhamos um ímã NS colocado em um campo magnético uniforme  . A massa magnética norte do ímã fica sujeita a uma força . A massa magnética norte do ímã fica sujeita a uma força  de mesma direção e sentido que o campo de mesma direção e sentido que o campo  . A massa magnética sul fica sujeita a uma força . A massa magnética sul fica sujeita a uma força  , de mesma direção que o campo, mas, sentido oposto. Essa força , de mesma direção que o campo, mas, sentido oposto. Essa força  é dada por: é dada por:
E, em módulo:  . .
A força que atua na massa magnética sul tem igual módulo (por isso a representamos por  ). As forças ). As forças  e e  tendo igual módulo, mesma direção e sentido opostos,
formam um binário. Esse binário tende a fazer o ímã
entrar em rotação no sentido indicado na figura acima.
Sabemos, da Mecânica,
que o momento de um binário é igual ao produto do
módulo de uma das forças pela distância entre as
forças.
Representando por C a esse momento, temos:
Sendo
tendo igual módulo, mesma direção e sentido opostos,
formam um binário. Esse binário tende a fazer o ímã
entrar em rotação no sentido indicado na figura acima.
Sabemos, da Mecânica,
que o momento de um binário é igual ao produto do
módulo de uma das forças pela distância entre as
forças.
Representando por C a esse momento, temos:
Sendo  o comprimento do ímã e o comprimento do ímã e  o ângulo que o eixo do ímã faz com a direção do campo, temos:
Fica:
Mas, o ângulo que o eixo do ímã faz com a direção do campo, temos:
Fica:
Mas,  módulo do momento magnético do ímã. Resulta: módulo do momento magnético do ímã. Resulta:

Esse conjugado
imprime ao ímã um movimento de rotação, até
que o ímã tome uma posição na qual o ângulo
 se anula. Nessa posição, se anula. Nessa posição,  , e o conjugado se anula (fig. 244). Mas, o
ímã não pára bruscamente, por causa da
inércia; atingindo a posição indicada na
figura 244 ele continua o seu movimento, passando
além da posição de equilíbrio. Mas, quando passa
dessa posição, o conjugado atua em sentido oposto e
faz o ímã voltar (fig. 245). Isso acontece
diversas vezes, isto é, o ímã entra em oscilação, e
depois pára com o seu eixo na direção do
campo. É isso o que acontece com a
bússola; ela oscila várias vezes e depois pára com
o eixo na direção do campo magnético terrestre,
pois este, em pequena extensão, pode ser
considerado uniforme.
, e o conjugado se anula (fig. 244). Mas, o
ímã não pára bruscamente, por causa da
inércia; atingindo a posição indicada na
figura 244 ele continua o seu movimento, passando
além da posição de equilíbrio. Mas, quando passa
dessa posição, o conjugado atua em sentido oposto e
faz o ímã voltar (fig. 245). Isso acontece
diversas vezes, isto é, o ímã entra em oscilação, e
depois pára com o seu eixo na direção do
campo. É isso o que acontece com a
bússola; ela oscila várias vezes e depois pára com
o eixo na direção do campo magnético terrestre,
pois este, em pequena extensão, pode ser
considerado uniforme.


Suponhamos um pólo plano com densidade magnética  e um ponto A infinitamente próximo desse polo. O
cálculo do campo magnético nesse ponto A é idêntico ao
cálculo do campo elétrico num ponto próximo de um plano
uniformemente eletrizado (veja o tópico "Campo Elétrico em um Ponto Próximo de um Plano" ). Chegamos à seguinte conclusão:
e um ponto A infinitamente próximo desse polo. O
cálculo do campo magnético nesse ponto A é idêntico ao
cálculo do campo elétrico num ponto próximo de um plano
uniformemente eletrizado (veja o tópico "Campo Elétrico em um Ponto Próximo de um Plano" ). Chegamos à seguinte conclusão:
1. Módulo do campo
Vale:
2. Direção
Perpendicular ao polo.
3. Sentido
Do polo para o ponto A se for polo norte; do ponto A para o polo, se for polo sul:

É muito
importante para nós o caso em que um polo plano norte é
situado infinitamente próximo e paralelo a um polo plano
sul, e com suas densidades magnéticas de mesmo valor
absoluto:  no polo sul (fig. 247). Considerando-se um ponto A
entre os dois planos, se existisse só o polo norte ele
produziria em A um campo magnético de módulo
no polo sul (fig. 247). Considerando-se um ponto A
entre os dois planos, se existisse só o polo norte ele
produziria em A um campo magnético de módulo
 , ,
perpendicular aos
polos e dirigido do polo norte para o polo sul.
Se existisse só o polo sul, ele produziria em A um campo
magnético de valor absoluto igual a esse  , também perpendicular aos polos e dirigido do polo norte
para o polo sul. Então os dois polos produzem em A
campos iguais. O campo resultante em A será o dobro de
, também perpendicular aos polos e dirigido do polo norte
para o polo sul. Então os dois polos produzem em A
campos iguais. O campo resultante em A será o dobro de  , isto é, será perpendicular aos polos, será dirigido do
polo norte para o polo sul, e terá por módulo:
ou
, isto é, será perpendicular aos polos, será dirigido do
polo norte para o polo sul, e terá por módulo:
ou
|
|

Indução magnética ou densidade de fluxo magnético
|
Além do vetor campo magnético  , existe no campo magnético uma outra grandeza vetorial,
que desempenha papel importantíssimo em muitos fenômenos
eletromagnéticos. É chamada indução magnética,
ou densidade de fluxo magnético e representada por
, existe no campo magnético uma outra grandeza vetorial,
que desempenha papel importantíssimo em muitos fenômenos
eletromagnéticos. É chamada indução magnética,
ou densidade de fluxo magnético e representada por  . .
Definição
Chama-se indução
magnética em um ponto ao produto da
permeabilidade magnética do meio pelo campo magnético
nesse ponto.
Isto é,
|
Características de B
A direção e o sentido da indução são a própria direção e sentido do campo magnético  . O módulo é igual ao produto de . O módulo é igual ao produto de  pelo módulo de pelo módulo de  , isto é, , isto é,
Admitindo-se que o campo seja produzido por uma massa magnética puntiforme, o módulo de  é: é:
Logo
ou
Concluímos que, quando o campo magnético É PRODUZIDO POR UM ÍMÃ, a indução  num ponto depende exclusivamente da massa magnética que
produz o campo e da distância do ponto à massa magnética,
MAS NÃO DEPENDE DO MEIO.
Unidades de indução magnética
num ponto depende exclusivamente da massa magnética que
produz o campo e da distância do ponto à massa magnética,
MAS NÃO DEPENDE DO MEIO.
Unidades de indução magnética
a. Sistema CGSES
A unidade de  é obtida considerando-se: é obtida considerando-se:
 (portanto, vácuo) (portanto, vácuo)
Resulta:
Um
gauss é a indução magnética num ponto de um campo
magnético no vácuo no qual a intensidade do campo é um
oersted.
Observações
1a) Pelo fato de ser  é que a unidade de permeabilidade magnética do
CGSEM também é chamada gauss/oersted, conforme
vimos no tópico "Sistema de Unidades de Magnetismo e Eletromagnetismo" .
é que a unidade de permeabilidade magnética do
CGSEM também é chamada gauss/oersted, conforme
vimos no tópico "Sistema de Unidades de Magnetismo e Eletromagnetismo" .
2a) É fácil provar que a indução magnética,  , é grandeza física da mesma espécie que a intensidade de imantação, , é grandeza física da mesma espécie que a intensidade de imantação,  , temos:
ou,
ou , temos:
ou,
ou
|
Indução e imantação
representam ambas o quociente de uma massa magnética
por uma área (ou quadrado de um comprimento, que é o
mesmo). Esse é o motivo pelo qual essas duas grandezas
são avaliadas nas mesmas unidades. No no tópico "Densidade Magnética"
provamos que densidade magnética é grandeza da mesma
espécie que a imantação, e que por isso também tem a mesma
unidade que esta. Na verdade, o nome gauss
originalmente foi dado à unidade de  , e depois passou a ser usado nas outras. , e depois passou a ser usado nas outras.
b. Sistema MKS
A unidade de  é deduzida considerando-se:
Resulta:
A unidade de é deduzida considerando-se:
Resulta:
A unidade de  no sistema MKS é chamada no sistema MKS é chamada  , é a indução magnética num ponto de um campo magnético
em que a intensidade do campo é um praoersted, num meio em
que a permeabilidade magnética é
, é a indução magnética num ponto de um campo magnético
em que a intensidade do campo é um praoersted, num meio em
que a permeabilidade magnética é  .
Podemos concluir que o produto de .
Podemos concluir que o produto de  por um praoersted dá por um praoersted dá  , do seguinte modo: já vimos, que , do seguinte modo: já vimos, que  .
Então:
Considerando a fórmula de Coulomb,
e escrevendo as unidades das grandezas, temos:
de onde tiramos que: .
Então:
Considerando a fórmula de Coulomb,
e escrevendo as unidades das grandezas, temos:
de onde tiramos que:
Então:
|
Linhas de indução
|
Chama-se linha de indução a uma linha que em todos os pontos é tangente ao vetor indução
|
Sendo o vetor  de mesma direção que o vetor de mesma direção que o vetor  , a linha de indução em cada ponto é também tangente ao vetor , a linha de indução em cada ponto é também tangente ao vetor  . Concluímos, então, que a linha da indução coincide com
a linha de força. Mas, usamos a expressão linha de força
quando nos referimos ao campo magnético
. Concluímos, então, que a linha da indução coincide com
a linha de força. Mas, usamos a expressão linha de força
quando nos referimos ao campo magnético  ; e a expressão linha de indução, quando nos referimos à induçao magnética ; e a expressão linha de indução, quando nos referimos à induçao magnética  .
As
linhas de indução têm então as mesmas características
que as linhas de força. Assim, em um campo
magnético uniforme as linhas de indução são retas e
paralelas. .
As
linhas de indução têm então as mesmas características
que as linhas de força. Assim, em um campo
magnético uniforme as linhas de indução são retas e
paralelas.
Fluxo magnético num campo uniforme
|
Suponhamos uma
superfície plana de área S colocada em um campo
magnético uniforme de indução magnética  . Seja n a normal à superfície e . Seja n a normal à superfície e  o ângulo que a normal à superfície faz com a direção do campo, que é a direção de o ângulo que a normal à superfície faz com a direção do campo, que é a direção de  (fig. 249). (fig. 249).
Definção
Chama-se fluxo
magnético que atravessa uma superfície plana,
colocada em um campo magnético uniforme, ao
produto do módulo de indução magnética, pela
área da superfície, pelo coseno do ângulo que a
normal à superfície faz com a direção do campo.
Representa-se o fluxo pela letra  . Então, por definição, . Então, por definição,
|
Vemos então que fluxo magnético é o fluxo da indução magnética  . .
Variação do fluxo
O fluxo
magnético pode variar por uma variação da área da
superfície, ou por uma variação da indução, ou por uma
variação da posição da superfície no campo. Dos três
processos, o mais comodo é o terceiro. Para isso fazemos a
superfície girar em torno de um eixo perpendicular ao
campo.
Essa variação do fluxo em função do ângulo  é idêntica à variação do fluxo elétrico em função do ângulo é idêntica à variação do fluxo elétrico em função do ângulo  , que foi estudada no tópico "Fluxo Elétrico num Campo Uniforme".
Devido à importância do assunto, sugerimos ao leitor que
reproduza a variação do fluxo em função de , que foi estudada no tópico "Fluxo Elétrico num Campo Uniforme".
Devido à importância do assunto, sugerimos ao leitor que
reproduza a variação do fluxo em função de  , mas, agora para o fluxo de , mas, agora para o fluxo de  . O gráfico da variação é o a seguir : . O gráfico da variação é o a seguir :
Queremos salientar
aqui que, na prática, o conhecimento da variação do
fluxo magnético é muito mais importante do que o
conhecimento da variação do fluxo elétrico. Porque a
variação do fluxo magnético é responsável pelo
importantíssimo fenômeno chamado indução eletromagnética,
que será estudado no Capítulo 16.
Unidades de fluxo magnético - 1. Sistema CGSEM
Esta unidade é obtida a partir da equação de definição considerando-se:
 , ou seja , ou seja  , o que significa superfície perpendicular ao campo. , o que significa superfície perpendicular ao campo.
Resulta:
Chama-se maxwell ao fluxo magnético que atravessa uma superfície plana de um  colocada perpendicularmente a um campo magnético uniforme de indução magnética um gauss. colocada perpendicularmente a um campo magnético uniforme de indução magnética um gauss.
Unidades de fluxo magnético - 2. Sistema MKS
A unidade de fluxo é obtida considerando-se:
Resulta:
Um
weber é o fluxo magnético que atravessa uma superfície
plana de área de um metro quadrado, colocada
perpendicularmente a um campo magnético uniforme de
indução magnética de um weber por metro quadrado
NOTA:
O termo weber originalmente foi empregado para designar
a unidade de fluxo magnético. Pelo fato de
ser
é que a unidade  é chamada é chamada  . .
No tópico "Sistema de Unidades de Magnetismo e Eletromagnetismo"
vimos que a unidade de massa magnética também é chamada
weber. Faz-se isso porque massa magnética e fluxo
magnético são grandezas físicas da mesma espécie.
Deixamos ao leitor, como exercício, demonstrar isso.
O fenômeno de indução magnética

Sabemos que a
intensidade de imantação de um ímã tem sempre o
sentido do polo sul para o polo norte (veja o tópico "Imantação ou Intensidade de Imantação ou Intensidade de Magnetização"); a intensidade de imantação do induzido tem o sentido  . Então neste primeiro caso, a intensidade de imantação . Então neste primeiro caso, a intensidade de imantação  do induzido tem o mesmo sentido que o campo indutor do induzido tem o mesmo sentido que o campo indutor  . .
2º Caso
Imaginemos colocada no campo indutor  uma barra de cobre, bismuto, ou grafite, por exemplo. Nessas substâncias, o polo sul uma barra de cobre, bismuto, ou grafite, por exemplo. Nessas substâncias, o polo sul  induzido aparece do lado do polo sul indutor, e o polo norte induzido aparece do lado do polo sul indutor, e o polo norte  induzido aparece do lado do polo norte indutor como
indica a figura 252. Neste caso, a intensidade de
imantação
induzido aparece do lado do polo norte indutor como
indica a figura 252. Neste caso, a intensidade de
imantação  do induzido tem sentido oposto ao do campo do induzido tem sentido oposto ao do campo  indutor. indutor.
Estas relações, entre os sentidos de  e o de e o de  indutor, são muito importantes. indutor, são muito importantes.

Sucetibilidade magnética
Classificação das substâncias magnéticas
|
As substâncias magnéticas dividem-se em três grupos.
1ª - Substâncias paramagnéticas
Por definição, são aquelas que têm susceptibilidade magnética positiva e constante.
Sendo  concluímos que:
a) concluímos que:
a)  positiva significa que positiva significa que  tem o mesmo sentido que tem o mesmo sentido que  , isto é, uma substância paramagnética sofre indução do 1o caso.
b) , isto é, uma substância paramagnética sofre indução do 1o caso.
b)  sendo constante, concluímos que sendo constante, concluímos que  é diretamente proporcional a é diretamente proporcional a  ; quanto mais forte for o campo indutor, maior será a imantaçao ; quanto mais forte for o campo indutor, maior será a imantaçao  .
Exemplos importantes
de substâncias diamagnéticas são: alumen
ferroso-amoniacal, alumínio, chumbo, cloreto cúprico,
cloreto férrico, oxigênio, etc.. .
Exemplos importantes
de substâncias diamagnéticas são: alumen
ferroso-amoniacal, alumínio, chumbo, cloreto cúprico,
cloreto férrico, oxigênio, etc..
2ª - Substâncias diamagnéticas
Por definição, são aquelas que têm susceptibilidade magnética negativa e constante.
Sendo  concluímos que :
a) concluímos que :
a)  negativa significa que negativa significa que  tem sentido oposto ao de tem sentido oposto ao de  , isto é, uma substância diamagnética sofre indução, do 2o caso.
b) , isto é, uma substância diamagnética sofre indução, do 2o caso.
b)  sendo constante, concluímos que sendo constante, concluímos que  é diretamente proporcional a é diretamente proporcional a  ; quanto mais forte for o campo indutor, maior será a imantação ; quanto mais forte for o campo indutor, maior será a imantação  .
Exemplos importantes
de substâncias diamagnéticas são: a grafite, o
bismuto, o cobre, prata, zinco, mercúrio, nitrogênio,
etc.. .
Exemplos importantes
de substâncias diamagnéticas são: a grafite, o
bismuto, o cobre, prata, zinco, mercúrio, nitrogênio,
etc..
3ª - Substâncias ferromagnéticas
Por definição, são
aquelas que têm susceptibilidade positiva, mas não
constante: a sua susceptibilidade é função do campo
indutor  .
Sendo .
Sendo  positivo, concluimos que positivo, concluimos que  tem o mesmo sentido que tem o mesmo sentido que  , isto é, uma substância ferromagnética também sofre indução do 1o caso (fig. 251). Mas, sendo , isto é, uma substância ferromagnética também sofre indução do 1o caso (fig. 251). Mas, sendo  variável, a imantação variável, a imantação  não é mais proporcional a não é mais proporcional a  . Obtemos experimentalmente os valores de . Obtemos experimentalmente os valores de  do induzido em função do campo indutor do induzido em função do campo indutor  , e depois levamos os resultados a um gráfico. Esse
gráfico é chamado curva de imantação. Está esquematizado
na figura 253. Essa curva mostra que, partindo de um
campo magnético indutor
, e depois levamos os resultados a um gráfico. Esse
gráfico é chamado curva de imantação. Está esquematizado
na figura 253. Essa curva mostra que, partindo de um
campo magnético indutor  nulo e aumentando esse campo, a imantação nulo e aumentando esse campo, a imantação  também vai aumentando. Mas, no começo, uma variação também vai aumentando. Mas, no começo, uma variação  do campo produz certa variação do campo produz certa variação  da imantação; quando o campo já possui um valor grande, a mesma variação da imantação; quando o campo já possui um valor grande, a mesma variação  do campo produz na imantação uma variação do campo produz na imantação uma variação  menor. menor.

Outro fato importante que essa curva nos mostra é que existe um valor  do campo para o qual a imantação atinge um valor máximo.
Daí por diante, continuando a aumentar o campo, a i
mantação não varia mais. Dizemos que a substância
atingiu a saturação. O valor máximo
do campo para o qual a imantação atinge um valor máximo.
Daí por diante, continuando a aumentar o campo, a i
mantação não varia mais. Dizemos que a substância
atingiu a saturação. O valor máximo  da imantação é chamado imantação de saturação. O valor da imantação é chamado imantação de saturação. O valor  do campo correspondente é chamado campo de saturação. O
ponto A correspondente do gráfico é chamado ponto de
saturação.
Substâncias ferromagnéticas são o ferro e muitas ligas de ferro.
do campo correspondente é chamado campo de saturação. O
ponto A correspondente do gráfico é chamado ponto de
saturação.
Substâncias ferromagnéticas são o ferro e muitas ligas de ferro.
Indução magnética em um ponto infinitamente próximo de um pólo plano
|
No tópico "Campo Magnético em um ponto Infinitamente Próximo de um Polo Plano" vimos que o campo magnético em um ponto infinitamente próximo de um polo plano é dado pela fórmula:
em que  é a permeabilidade do meio em que se produz o campo e é a permeabilidade do meio em que se produz o campo e  é a intensidade de imantação do ímã que produz o campo.
De acordo com a definição de indução magnética, nesse ponto ela valerá: é a intensidade de imantação do ímã que produz o campo.
De acordo com a definição de indução magnética, nesse ponto ela valerá:
 , ,
ou
ou
Note-se
que essa indução magnética depende exclusivamente da
intensidade de imantação do ímã que produz o campo, e
não depende do meio.
A direção e o sentido de  sempre concordam com a direção e o sentido de sempre concordam com a direção e o sentido de 
|
Vimos também que,
quando existe um polo norte plano paralelo a um polo
sul plano, infinitamente próximos e com densidades
magnéticas de mesmo valor absoluto (fig. 255), o campo
magnético em um ponto situado entre eles é dado pela
fórmula:
Então a indução nesse ponto será:
ou
ou
Indução magnética no interior de um imã
Na
indução magnética produzida em A devida à magnetização da
própria barra só influem as partes da barra infinitamente
próximas do ponto A. Imaginemos então traçada no interior
do ímã uma cavidade retangular de lados infinitamente
próximos, perpendicular ao campo e contendo o ponto A no
seu interior (fig. 256).
Sabemos que, quando
cortamos o ímã, os seus polos não ficam isolados, mas
nos lugares de corte aparecem novos polos de
densidades magnéticas iguais às dos polos primitivos.
Assim, na cavidade retangular aparecerão polos  e e  de densidades magnéticas de densidades magnéticas  e e  respectivamente.
O ponto
A estará então entre dois polos planos, paralelos,
infinitamente próximos e de densidades magnéticas respectivamente.
O ponto
A estará então entre dois polos planos, paralelos,
infinitamente próximos e de densidades magnéticas  e e  . Já vimos que nessas condições esses polos produzem em A uma indução magnética igual a . Já vimos que nessas condições esses polos produzem em A uma indução magnética igual a  , de acordo com a fórmula (153).
Então a indução no ponto será a soma de , de acordo com a fórmula (153).
Então a indução no ponto será a soma de  com com  , isto é, será:
ou
Sendo , isto é, será:
ou
Sendo  a susceptibilidade da barra imantada, sabemos que a susceptibilidade da barra imantada, sabemos que  . Substituindo na fórmula anterior, ela fica:
ou
As expressões . Substituindo na fórmula anterior, ela fica:
ou
As expressões  e e  dão, portanto, a indução magnética no interior de um ímã
em função da susceptibilidade magnética do ímã, da
permeabilidade magnética do vácuo e do campo indutor
dão, portanto, a indução magnética no interior de um ímã
em função da susceptibilidade magnética do ímã, da
permeabilidade magnética do vácuo e do campo indutor  suposto no vácuo.
Suponhamos que uma barra de permeabilidade magnética suposto no vácuo.
Suponhamos que uma barra de permeabilidade magnética  seja colocada num campo magnético de intensidade seja colocada num campo magnético de intensidade  , produzido no vácuo. Essa barra adquirirá uma indução magnética B, que está ligada a , produzido no vácuo. Essa barra adquirirá uma indução magnética B, que está ligada a  pela relação:
Comparando com a fórmula pela relação:
Comparando com a fórmula  temos :
Concluímos que a
permeabilidade magnética de uma substância é igual à
soma da permeabilidade magnética do vácuo com temos :
Concluímos que a
permeabilidade magnética de uma substância é igual à
soma da permeabilidade magnética do vácuo com  vezes a susceptibilidade magnética da substância. vezes a susceptibilidade magnética da substância.
Histerese
|
A curva de  em função de em função de  para uma substância ferromagnética, mostrada na figura 253, e no tópico "Classificação da Substâncias Magnéticas",
é obtida desde que a substância esteja inicialmente
desimantada e a intensidade do campo seja aumentada
gradualmente a partir de zero. Suponhamos que,
partindo de zero, vamos aumentando a intensidade do campo
até o valor de saturação, para uma substância ferromagnética, mostrada na figura 253, e no tópico "Classificação da Substâncias Magnéticas",
é obtida desde que a substância esteja inicialmente
desimantada e a intensidade do campo seja aumentada
gradualmente a partir de zero. Suponhamos que,
partindo de zero, vamos aumentando a intensidade do campo
até o valor de saturação,  . Obtemos a curva OP (fig. 257). Enquanto estamos
aumentando o campo, a um valor H do campo corresponde o
valor I da imantação. Se, a partir do valor de saturação
. Obtemos a curva OP (fig. 257). Enquanto estamos
aumentando o campo, a um valor H do campo corresponde o
valor I da imantação. Se, a partir do valor de saturação
 , vamos diminuindo o campo até que ele se anule, a curva de volta não é PO mas, é , vamos diminuindo o campo até que ele se anule, a curva de volta não é PO mas, é  . De maneira que, para o mesmo valor H do campo a imantação tem o valor . De maneira que, para o mesmo valor H do campo a imantação tem o valor  maior do que I. Quando o campo se anula, a imantação se mantém com um valor maior do que I. Quando o campo se anula, a imantação se mantém com um valor  . .
|
Portanto, para um
mesmo valor do campo, a imantação tem valor maior
quando o campo decresce do que quando o campo cresce.
Esse fenômeno é chamado histerese. (Histerese significa
“atraso”).
Querendo desimantar a substância, isto é, anular a imantação  , precisamos aplicar um campo magnético em sentido oposto. Quando o campo atingir certo valor , precisamos aplicar um campo magnético em sentido oposto. Quando o campo atingir certo valor  a imantação se anula. Aumentando esse campo em sentido
oposto, a imantação cresce outra vez a partir de zero, mas
em sentido oposto até atingir novamente a saturação,
(parte negativa do gráfico, até o ponto M).
Diminuindo outra vez o campo, a imantação vai diminuindo;
quando o campo se anula, a imantação mantém um valor
a imantação se anula. Aumentando esse campo em sentido
oposto, a imantação cresce outra vez a partir de zero, mas
em sentido oposto até atingir novamente a saturação,
(parte negativa do gráfico, até o ponto M).
Diminuindo outra vez o campo, a imantação vai diminuindo;
quando o campo se anula, a imantação mantém um valor  . .
Aumentando outra vez o campo no sentido primitivo, quando ele atinge o valor  a imantação se anula. a imantação se anula.
O
conjunto de todos os valores de H e I necessários para
formar a curva fechada é chamado ciclo de histerese. O
valor  da imantação é chamado RETENTIVIDADE, ou REMANÊNCIA, ou
IMANTAÇÃO REMANENTE, ou IMANTAÇÃO REMANESCENTE. O valor
da imantação é chamado RETENTIVIDADE, ou REMANÊNCIA, ou
IMANTAÇÃO REMANENTE, ou IMANTAÇÃO REMANESCENTE. O valor
 do campo é chamado COERCIVIDADE, ou CAMPO COERCITIVO, ou
FORÇA COERCITIVA. (Apesar de não ser uma
força).
do campo é chamado COERCIVIDADE, ou CAMPO COERCITIVO, ou
FORÇA COERCITIVA. (Apesar de não ser uma
força).
Curva - B-H
| Β |
Em vez de representarmos graficamente a intensidade de imantação  do ímã em função do campo indutor do ímã em função do campo indutor  podemos representar a indução magnética podemos representar a indução magnética  no ímã em função do campo indutor no ímã em função do campo indutor  . Essa curva que dá . Essa curva que dá  em função do em função do  é chamada curva B-H, ou curva de imantação. é chamada curva B-H, ou curva de imantação.
A curva B-H tem o mesmo aspecto da curva que dá  em função de em função de  . Ela também descreve o ciclo de histerese. Isso era de se esperar, pois vimos que: . Ela também descreve o ciclo de histerese. Isso era de se esperar, pois vimos que:
Cada ponto da curva corresponde à soma de um termo igual à  com um termo igual a com um termo igual a  , como está indicado na figura 258. Quando o ímã atinge a
saturação, I fica constante por mais que aumentemos
, como está indicado na figura 258. Quando o ímã atinge a
saturação, I fica constante por mais que aumentemos  ; então ; então  também fica constante. Mas, a curva B-H não fica paralela ao eixo do também fica constante. Mas, a curva B-H não fica paralela ao eixo do  , por causa do termo , por causa do termo  . À medida que aumentamos . À medida que aumentamos  , o termo , o termo  aumenta. Então, na região de saturação, a curva B-H se torna uma reta, mas não paralela ao eixo do aumenta. Então, na região de saturação, a curva B-H se torna uma reta, mas não paralela ao eixo do  . .
|
Ponto curie ou temperatura curie
|
As
propriedades magnéticas das substâncias ferromagnéticas
variam muito com a temperatura. Aumentando a
temperatura, as propriedades magnéticas diminuem.
Para cada substância ferromagnética existe uma
temperatura na qual ela se desimanta por completo. Essa
temperatura é chamada PONTO CURIE. Exemplos de alguns
pontos Curie:
para o ferro 770oC
para o níquel 354oC
para a magnética 580oC
para o cobalto 1130oC
|
Magnetismo terrestre
|
Chama-se
campo magnético terrestre a esse campo magnético que
existe ao redor da Terra. A existência
desse campo se manifesta pela orientação da agulha
magnética. O campo magnético terrestre pode ser
considerado uniforme em uma extensão bastante grande
como, por exemplo, na região ocupada por uma cidade.
1. Definições
Suponhamos
que num certo lugar A (por exemplo, São
Paulo, ou Rio de Janeiro) uma agulha
magnética seja suspensa pelo centro de
gravidade, de maneira que ela possa girar
livremente. A agulha se orienta de maneira
que seu eixo fique na linha de força do campo
magnético. Essa linha de força em cada lugar é
muito próxima da linha norte-sul geográfica
(meridiano geográfico), mas não coincide
com ela, conforme veremos.
Chama-se
plano meridiano magnético do lugar A ao
plano vertical que passa pelo eixo da
agulha.
Chama-se
meridiano magnético do lugar à interseção
do plano meridiano magnético com o globo
terrestre.
|
|
Chama-se
declinação magnética do lugar ao ângulo d formado pelo
meridiano magnético com o meridiano geográfico
(fig. 259). A declinação é chamada oriental
quando o polo norte da agulha se acha no oriente do
meridiano geográfico; é o caso da figura 259. É
ocidental no caso contrário.,
Chama-se
inclinação magnética do lugar ao ângulo i que a agulha
faz com o plano horizontal (fig. 260). A inclinação é
considerada positiva quando o polo norte da agulha
está abaixo do plano horizontal; é o caso da figura
260. É negativa no caso contrário.
2. Componentes horizontal e vertical
Costuma-se decompor o campo magnético terrestre  em duas componentes: uma, horizontal em duas componentes: uma, horizontal  , e outra vertical , e outra vertical  (fig. 261). (fig. 261).
Vê-se claramente que:

em que  é a inclinação magnética do lugar. é a inclinação magnética do lugar.
|

3. Mapas magnéticos
Em
todos os países se fazem medidas do campo magnético
H, da declinação d e da inclinação i praticamente em
todo o território. Os valores encontrados
são assinalados em mapas. Depois se traça uma
linha pelos lugares onde a declinação tem o mesmo
valor; outra pelos lugares em que a inclinação tem o
mesmo valor, etc.. Chamam-se linhas isógonas, àquelas
que unem pontos nos quais a declinação tem o mesmo
valor. Chamam-se linhas isóclinas àquelas que unem
pontos nos quais a inclinação tem o mesmo
valor. Chamam-se linhas isodinâmicas àquelas que
unem pontos em que a componente horizontal  do campo tem o mesmo valor. do campo tem o mesmo valor.
4. Variação do campo magnético terrestre
A declinação, a inclinação e o campo  variam de um lugar para outro, e também variam num
mesmo lugar. Em um mesmo lugar se observam
variações diurnas do campo, que assinalam
pequenas oscilações. E variações mais profundas, que
alteram por completo os valores de H, d e i,
observadas ao cabo de muitos anos; estas se chamam
variações seculares.
Às
vezes há variações muito bruscas e muito intensas
observadas no campo magnético, e que são
percebidas não em um único lugar, mas em todos os
observatórios magnéticos da Terra. Essas variações
bruscas são chamadas tempestades magnéticas. O seu
aparecimento coincide com as auroras polares. Tem-se
quase como certo que o aparecimento brusco de uma
mancha solar acarreta uma tempestade magnética.
variam de um lugar para outro, e também variam num
mesmo lugar. Em um mesmo lugar se observam
variações diurnas do campo, que assinalam
pequenas oscilações. E variações mais profundas, que
alteram por completo os valores de H, d e i,
observadas ao cabo de muitos anos; estas se chamam
variações seculares.
Às
vezes há variações muito bruscas e muito intensas
observadas no campo magnético, e que são
percebidas não em um único lugar, mas em todos os
observatórios magnéticos da Terra. Essas variações
bruscas são chamadas tempestades magnéticas. O seu
aparecimento coincide com as auroras polares. Tem-se
quase como certo que o aparecimento brusco de uma
mancha solar acarreta uma tempestade magnética.
Resumo das unidades estudadas nesse capítulo
Grandeza
|
Símbolo
|
Unidade CGSEM
|
Unidade MKS
|
| Intensidade de campo magnético |
|
oersted
|
praoersted, ou 
|
| Indução magnética |
|
Gauss
|
|
| Fluxo magnético |
|
Maxwell
|
Weber
|
| Susceptibilidade magnética |
|
|
|
Nota: É útil relembrar que:
 e e  têm as mesmas unidades; têm as mesmas unidades;
 , ,  e e  têm as mesmas unidades; têm as mesmas unidades;
 e m têm as mesmas unidades . e m têm as mesmas unidades .
|
Massa Magnética
|
Assim
como em Eletrostática introduzimos o conceito de carga
elétrica para podermos medir a força entre corpos
eletrizados, em magnetismo introduzimos o conceito de
massa magnética para que possamos medir a força entre
corpos imantados. E, analogamente ao que acontece com
carga elétrica, não temos elementos para dar uma definição
de massa magnética. Consideramo-la um conceito primitivo
e fixamos uma convenção que nos permite dizer quando duas
massas magnéticas são iguais, ou uma é múltipla da
outra. Do mesmo modo que no caso da carga
elétrica, para fixarmos o critério de igualdade e
multiplicidade de duas massas magnéticas precisamos
considerar massas magnéticas ideais, chamadas massas
magnéticas puntiformes. Massa magnética puntiforme é
aquela contida em uma região polar cujas dimensões possam
ser desprezadas relativamente ao problema em que está
sendo considerada; em outras palavras, a região polar fica
reduzida a um ponto.
Critérios de igualdade e multiplicidade
Suponhamos
que desejamos comparar a massa magnética da
região polar N do ímã 1 com a massa
magnética da região polar N do ímã 2. Para
isso usamos um terceiro ímã, o ímã 3 (fig. 226), e
avaliamos a força que os polos norte de 1 e 2
exercem sobre o polo sul, por exemplo, do
ímã 3. Quando o ímã 3 é colocado
próximo do ímã 1, não vai haver ação só da região N
de 1 sobre a região S de 3, mas sim, das duas
regiões de 1 sobre as duas regiões de 3. Como nos
interessa saber só a ação de N de 1 sobre S de 3,
imaginamos os dois ímãs suficientemente
compridos para que possamos desprezar os
efeitos das regiões polares que não nos
interessam, que são a S de 1 e N de 3.
A região N de 1, colocada à distância d da região S de 3, em certo ambiente dá origem à força  . A região N de 2, colocada à mesma distância d da
região S de 3, no mesmo ambiente, dá origem à força
. A região N de 2, colocada à mesma distância d da
região S de 3, no mesmo ambiente, dá origem à força  . Relativamente aos módulos de . Relativamente aos módulos de  e e  há dois casos: há dois casos:
1o caso: 
2o caso: 
Convencionamos que, no 1o caso, a massa magnética da região N de 1 é igual à massa magnética da região N de 2. E que, no 2o
caso, a massa magnética da região N de 2 é igual a n
vezes a massa magnética da região N de 1. Representando
por  e e  respectivamente, essas massas magnéticas, temos: respectivamente, essas massas magnéticas, temos:
no 1o caso: 
no 2o caso: 
Escolhendo arbitrariamente a massa  como unidade, e adotando esse critério, podemos medir a massa magnética como unidade, e adotando esse critério, podemos medir a massa magnética  . No primeiro caso, teríamos . No primeiro caso, teríamos  ; no segundo caso, ; no segundo caso,  . .
Notas
1a)
É importante notar que os critérios de igualdade
e multiplicidade consistem em se medirem as
massas magnéticas por números proporcionais às
forças que essas massas magnéticas conseguem
exercer. Pois, sendo  ao mesmo tempo que ao mesmo tempo que  , temos: , temos:
2a) A região N de 1 exerce sobre a região S de 3 uma força  de atração, à distância d. Se colocarmos à
mesma distância d a região S de 1 e a região S
de 3, observaremos entre elas uma força de
repulsão de mesmo módulo que
de atração, à distância d. Se colocarmos à
mesma distância d a região S de 1 e a região S
de 3, observaremos entre elas uma força de
repulsão de mesmo módulo que  . E, se as regiões polares N e S de um mesmo ímã
nas mesmas condições exercem forças iguais,
concluímos que elas tem igual massa
magnética. Mas como uma exerce força de atração
quando a outra exerce força de repulsão,
convencionamos considerar positiva a massa magnética
da região N e negativa a da região S. Para um
mesmo ímã, temos, então:
. E, se as regiões polares N e S de um mesmo ímã
nas mesmas condições exercem forças iguais,
concluímos que elas tem igual massa
magnética. Mas como uma exerce força de atração
quando a outra exerce força de repulsão,
convencionamos considerar positiva a massa magnética
da região N e negativa a da região S. Para um
mesmo ímã, temos, então:
Leis de atração e repulsão entre massas magnéticas puntiformes
|
Suponhamos duas massas magnéticas puntiformes,  e e  , separadas pela distância d. As forças , separadas pela distância d. As forças  e e  que atuam nelas obedecem a duas leis, análogas àquelas
leis relativas a cargas elétricas puntiformes (veja o
tópico "Leis de Atração e Repulsão" ).
que atuam nelas obedecem a duas leis, análogas àquelas
leis relativas a cargas elétricas puntiformes (veja o
tópico "Leis de Atração e Repulsão" ).
|
|

1ª - Lei
| “A
intensidade da força de atração ou repulsão entre
duas massas magnéticas puntiformes é proporcional ao
produto das massas magnéticas.” |
Esta lei é uma
consequência do critério adotado para comparar duas
massas magnéticas. Repita aqui o raciocínio feito no
tópico "Leis de Atração e Repulsão".
2ª - Lei de Coulumb
| “A intensidade
da força de atração ou repulsão entre duas massas
magnéticas puntiformes é inversamente
proporcional ao quadrado da distância entre elas.” |
Fórmula de Coulomb
Pólo de um ímã
|
Já
vimos que um ímã só possui propriedades magnéticas em
certas regiões, que chamamos regiões polares norte e sul,
que elas possuem massas magnéticas de iguais valores
absolutos. Essas regiões polares de um ímã não são
pontos, mas são superfícies. As leis que estudamos
relativas à atração e repulsão, e a fórmula de Coulomb, só
valem para massas magnéticas puntiformes. Entretanto, no
caso de um ímã cujas massas magnéticas não são
puntiformes também podemos aplicar essas leis, pelo
seguinte motivo: a massa magnética norte está distribuída
pela região polar norte. Mas, nessa região existe um
ponto N tal que, se a massa magnética estivesse
concentrada nele, exerceria o mesmo efeito que exerce
quando está distribuída. Esse ponto N é chamado polo
norte. Do mesmo modo, polo sul é um ponto da
região polar sul tal que, se toda a massa magnética sul
estivesse concentrada nele, exerceria o mesmo efeito que
quando está distribuída.
Desse modo,
trabalhando com polos, podemos aplicar a fórmula de
Coulomb e todas as consequências que resultarão dela. Por
isso, daqui por diante nos referiremos aos polos e não
mais às regiões polares.
Definição
Chama-se comprimento de um ímã à distância entre seus polos; representaremos por  . . | | | | | | | | |
|
|
|
|
|
|
|
|
| | | | | | | | |
|

Inseparabilidade dos pólos
|
Os
polos de um ímã são inseparáveis. Se cortamos um ímã, os
polos norte e sul não ficam isolados. Na parte
correspondente ao polo norte aparece um novo polo sul; e
na parte correspondente ao polo sul primitivo aparece um
novo polo norte. Na natureza não existe um
único polo magnético norte ou sul isolado: eles sempre
existem aos pares, formando um ímã. Mas, muitas
vezes temos necessidade de estudar a influência de um
único polo magnético, norte ou sul. Nesse caso, supomos
um ímã muito comprido, de tal modo que possamos desprezar a
influência do polo norte sobre o polo sul, e
reciprocamente.
|
Sistemas de unidades em magnetismo e eletromagnetismo
|
Vimos, no tópico "Unidades de Carga Elétrica"
, que o sistema MKS contém unidades em toda a
Eletricidade, isto é, em Eletrostática, Eletrodinâmica,
Magnetismo e Eletromagnetismo. E que o sistema CGSES
contém unidades só em Eletrostática e Eletrodinâmica.
Além do CGSES, existe
um outro sistema de unidades elétricas derivado do
CGS mecânico: é chamado CGS eletromagnético
(abreviadamente, CGSEM). Este sistema se inicia em
Magnetismo, e é por isso que somente agora vamos
estudá-lo. Embora se chame CGS eletromagnético, ele
possui unidades também em Eletrostática e Eletrodinâmica,
mas nessas partes suas unidades não são usadas.
Sistema CGSEM - a. Unidades fundamentais
Recorde o tópico "Unidades de Carga Elétrica".
Já dissemos que não é possível construir-se um sistema
de unidades elétricas partindo-se exclusivamente das
três unidades fundamentais da Mecânica, mas, é
necessário adotar-se uma quarta unidade fundamental,
tipicamente elétrica. Esta quarta unidade do sistema
CGSEM é a de permeabilidade magnética.
O
sistema CGSEM adota arbitrariamente o valor 1 para a
permeabilidade magnética do vácuo. A unidade de
permeabilidade magnética deste sistema se indica por  , ou , ou  ; também é chamada gauss/oersted, por razões que veremos mais tarde. (Tópico "Indução Magnética ou Densidade de Fluxo Magnético") ; também é chamada gauss/oersted, por razões que veremos mais tarde. (Tópico "Indução Magnética ou Densidade de Fluxo Magnético")
As unidades fundamentais do sistema CGSEM são, portanto:
1) unidade de comprimento – centímetro
2) unidade de massa – grama
3) unidade de tempo – segundo
4) unidade de permeabilidade magnética – gauss/oersted, ou  . .
Sistema CGSEM - b. Unidade de massa magnética
É deduzida a partir da fórmula de Coulomb:
Considerando-se:
Portanto: a
unidade de massa magnética do sistema CGSEM é a massa
magnética puntiforme, que, colocada no vácuo a um
centímetro de outra massa magnética puntiforme igual,
exerce sobre ela a repulsão de um dine.
Nota:
A permeabilidade magnética do ar é muito próxima da do
vácuo. Na prática a consideramos também igual a
1 gauss/oersted.
Sistema MKS - a. Unidades fundamentais
Já vimos que
as unidades fundamentais deste sistema são: o
metro, o quilograma, o segundo e o
ampère. Agora que já sabemos o que é
permeabilidade magnética, podemos nos deter mais
na definição do ampère, já dada no tópico "A Formação do Sistema MKS em Eletricidade".
No estudaremos o seguinte fenômeno: quando dois
condutores, com corrente, são colocados próximos,
cada um deles exerce força sobre o outro.
Veremos
que se os condutores são retilíneos e paralelos,
as forças que atuam nos dois tem igual módulo que
vale:
onde:  e e  são as intensidades das correntes; são as intensidades das correntes;  é o comprimento dos condutores; a é a distância entre os condutores; é o comprimento dos condutores; a é a distância entre os condutores;  é a permeabilidade magnética do meio. é a permeabilidade magnética do meio.
|
|

Vimos que o ampère é
definido do seguinte modo: ampère é a
intensidade de uma corrente invariável que, passando em
dois condutores paralelos e de comprimento infinito e
distantes entre si de um metro, no vácuo, faz aparecer em
cada condutor a força de  newtons por cada metro de condutor. newtons por cada metro de condutor.
Sistema MKS - b. Unidade de permeabilidade magnética
É deduzida a partir da fórmula  . Tiramos: . Tiramos:
Se fizermos:
 Resulta: Resulta: 
ou
que é a unidade de permeabilidade deste sistema.
Sistema MKS - c. Permeabilidade magnética do vácuo
É calculada pela fórmula  ,
bastando para isso colocar nessa fórmula os valores das
grandezas que entram na definição de ampère. Isto é, se
considerarmos: ,
bastando para isso colocar nessa fórmula os valores das
grandezas que entram na definição de ampère. Isto é, se
considerarmos:
então o  será o do vácuo. Representaremos por será o do vácuo. Representaremos por  a permeabilidade do vácuo. Então: a permeabilidade do vácuo. Então:
ou
Nota:
A permeabilidade magnética do ar é muito próxima da
permeabilidade do vácuo. Na prática as
consideramos iguais.
Sistema MKS - d. Unidade de massa magnética
É deduzida a partir da fórmula de Coulomb, considerando-se:
Resulta:
A
unidade de massa magnética do sistema MKS é a massa
magnética puntiforme que, colocada no vácuo a um metro de
outra massa magnética puntiforme igual exerce a repulsão
de  . É chamada . É chamada  , e por razões que veremos mais adiante também é chamada weber (tópico "Fluxo Magnético num Campo Uniforme" ). , e por razões que veremos mais adiante também é chamada weber (tópico "Fluxo Magnético num Campo Uniforme" ).
Momento magnético de um imã
|
Consideremos um vetor cujo módulo seja o comprimento de ímã  , cuja direção seja a direção norte-sul do ímã, e cujo
sentido seja do polo sul para o polo norte.
Representaremos esse vetor por
, cuja direção seja a direção norte-sul do ímã, e cujo
sentido seja do polo sul para o polo norte.
Representaremos esse vetor por  . Chama-se momento magnético do ímã ao produto do vetor . Chama-se momento magnético do ímã ao produto do vetor  pelo valor absoluto da massa magnética de um dos polos.
Pela própria definição vemos que é uma grandeza vetorial.
Representando por
pelo valor absoluto da massa magnética de um dos polos.
Pela própria definição vemos que é uma grandeza vetorial.
Representando por  o momento magnético e por o momento magnético e por  o valor absoluto da massa magnética de um dos polos, temos: o valor absoluto da massa magnética de um dos polos, temos:
|
O módulo do momento magnético é:
 . .
Unidades - 1. Sistema CGSEM
A unidade de  é obtida considerando-se: é obtida considerando-se:
 e e 
Resulta:
A unidade CGSEM de  é o momento magnético de um ímã de um centímetro de comprimento que tenha em cada polo uma é o momento magnético de um ímã de um centímetro de comprimento que tenha em cada polo uma  . É também chamada . É também chamada  , como veremos no § seguinte. , como veremos no § seguinte.
Unidades - 2. Sistema MKS
É necessário considerar-se:
Resulta:
 . .
 é o momento magnético de um ímã de um metro de
comprimento que tenha em cada polo a massa magnética de um
weber.
é o momento magnético de um ímã de um metro de
comprimento que tenha em cada polo a massa magnética de um
weber.
Imantação ou intensidade de imantação ou intensidade de magnetização
Densidade magnética
|
Chama-se
densidade magnética de uma região polar ao quociente da
massa magnética, pela área da região. Sendo m a massa
magnética, S a área da região polar, a densidade
magnética será:
A
densidade magnética tem o sinal da massa magnética: é
positiva quando se trata de polo norte, negativa,
quando de polo sul.
Facilmente
se conclui que a intensidade de imantação é grandeza
física da mesma espécie que a densidade magnética.
Temos:
Por serem grandezas da mesma espécie,  e e  tem as mesmas unidades, isto é, gauss no CGSEM, e tem as mesmas unidades, isto é, gauss no CGSEM, e  no MKS. no MKS.
|
Relacão entre |I| e |σ| em um imã de forma de prismo reto
A forma mais
simples de um ímã é a de um prisma reto. Nesse ímã as regiões polares são
as bases do prisma. Sendo s a área da base,  o comprimento do ímã (que se confunde com a altura do prisma), temos: o comprimento do ímã (que se confunde com a altura do prisma), temos:
Isto é,
Chegamos a uma
conclusão importante: o módulo da imantação é igual
ao valor absoluto da densidade magnética dos polos.
Resumo das unidades estudadas até o momento:
Grandeza
|
Símbolo
|
Unidade CGSEM
|
Unidade MKS
|
| Permeabilidade magnética |
|
|
|
| Massa magnética |
m
|
|
Weber
|
| Momento magnético |
|
|
|
| Intensidade de imantação |
|
gauss
|
|
| Densidade magnética |
|
gauss
|
|
Permeabilidade magnética do vácuo:
Sistema CGSEM:
Sistema MKS:
Esses valores também podem ser usados como a permeabilidade do ar.
|
|
|
|










 Ímã de Neodímio é um poderoso ímã feito a
partir de uma combinação de neodímio, ferro e boro — Nd2Fe14B.
Esses ímãs são muito poderosos em comparação a sua massa, mas
também são mecanicamente frágeis e perdem seu magnetismo em
temperaturas acima de 120°C. Devido ao seu custo mais baixo, eles
têm substituído os ímãs de samário-cobalto na maioria das
aplicações, que são ligeiramente mais fracos e significativamente
mais resistentes a temperatura. Sua intensidade pode ser
medida pelo seu produto energético máximo, em megagauss-oersteds
(MGOe) (1 MGOe = 7,957 kJ/m3). Essa intensidade varia de 12 a 15,
nos ímãs aglomerados de neodímio (bonded magnets) e de 24 a 54 nos
ímãs sintetizados.
Ímã de Neodímio é um poderoso ímã feito a
partir de uma combinação de neodímio, ferro e boro — Nd2Fe14B.
Esses ímãs são muito poderosos em comparação a sua massa, mas
também são mecanicamente frágeis e perdem seu magnetismo em
temperaturas acima de 120°C. Devido ao seu custo mais baixo, eles
têm substituído os ímãs de samário-cobalto na maioria das
aplicações, que são ligeiramente mais fracos e significativamente
mais resistentes a temperatura. Sua intensidade pode ser
medida pelo seu produto energético máximo, em megagauss-oersteds
(MGOe) (1 MGOe = 7,957 kJ/m3). Essa intensidade varia de 12 a 15,
nos ímãs aglomerados de neodímio (bonded magnets) e de 24 a 54 nos
ímãs sintetizados.















































 (constante)
(constante)

 Resulta:
Resulta: 
 Resulta:
Resulta: 




